딥러닝을 위한 수치해석 제 2강[KNU 2022-1]
👨💻🏫KNU 2022-1 SW & media 수치해석 필기노트 2
0. Object-선형방정식의 계
\[AX=y, A= \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{pmatrix}, X= \begin{pmatrix} x_{1}\\ x_{2}\\ \vdots \\ x_{n} \end{pmatrix}, Y= \begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{m} \end{pmatrix}\]1. 행렬식
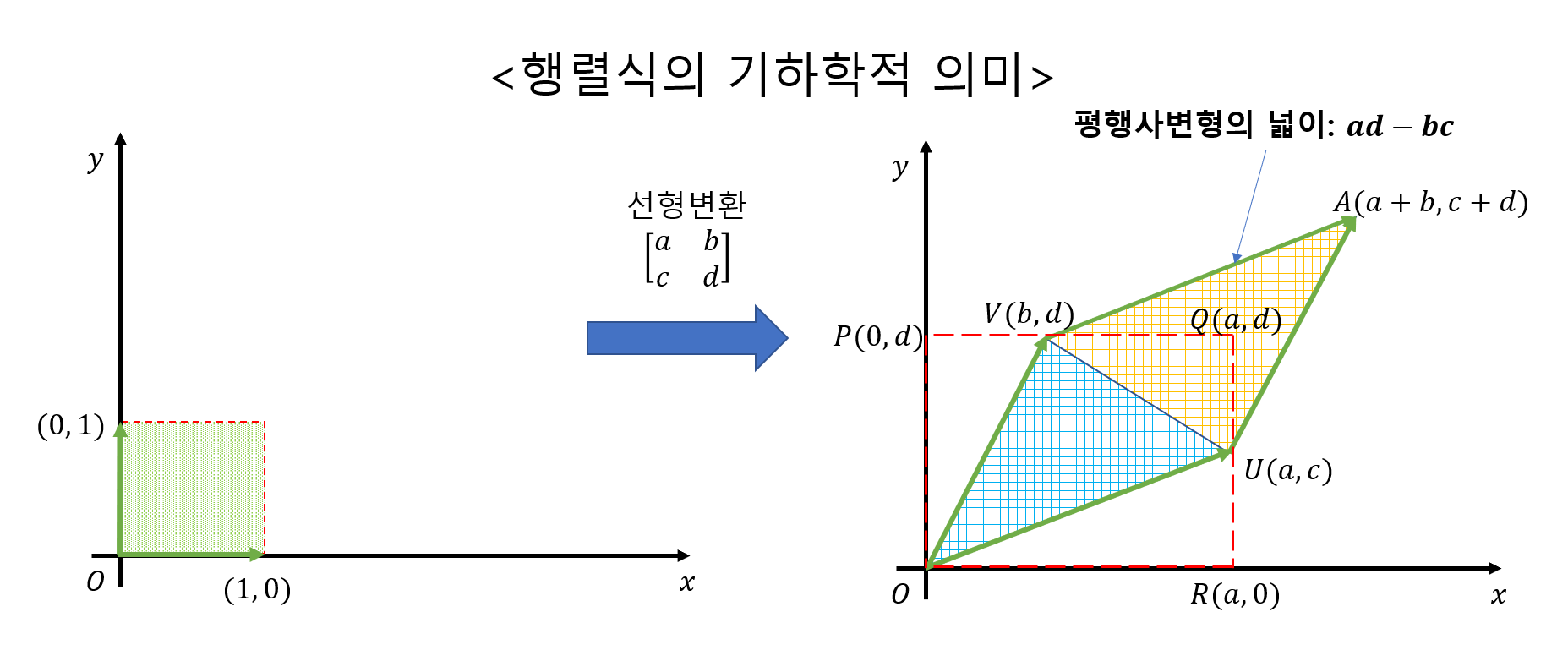
다음 2차 정방행렬($n=m=2$)에 관한 행렬식의 의미는, 행렬에 실수(스칼라)를 대응시킨것으로 det(A)와같이 표현한다.
\(A= \begin{pmatrix}a & b\\c & d\\\end{pmatrix}
\\
\\
A^{-1}= \frac{1}{ad-bc}\begin{pmatrix}d, -b\\ -c, a\end{pmatrix}
\\
\\
det(A)=ad-bc\)
A를 이용하여 각각의 두행을 가지고 벡터를 만들어본다면 이렇게 표현된다.
\[\vec{u}=(a,b), \vec{v}=(c,d)\]다음 평행사변형의 가로 길이는 다음과 같다
\[||\vec{u}||\]높이는 다음과 같다
\[sin\theta=\frac{h}{||\vec{v}||} \\ h=sin\theta\times||\vec{v}||\]즉 넓이는 $\theta’=90\degree-\theta$ 일때 이를 행렬식으로 표현하면
\[||\vec{u}||\times (sin\theta\times||\vec{v}||)\\ =||\vec{u}\bot||\times (cos\theta'\times||\vec{v}||)\\ =||\vec{u}\bot||\cdot ||\vec{v}||\\ =(-b,a)\cdot (c,d)\\ =ad-bc\\ =def(A)\]\[R_{90}= Rot90\degree(R\theta= \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{pmatrix} ) = \begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} a \\ b \\ \end{pmatrix} =\begin{pmatrix} -b \\ a \\ \end{pmatrix} =(-b,a)\]참고: 위의 (-b,a)의 도출식
2. 행렬식의 성질
1-해의 존재성과 유일성
- n개의 행렬이 독립이 아니라면 종속이라고 할 수 있다. 행렬식값이 0이냐 아니냐에 따라 주어진 행렬의 행벡터가 종속인지 아닌지 알수있다.
2-행렬 A가 정방행렬일때의 규칙성(동치)
- 행렬이 역행렬을 갖는다
- 행렬형 연립방정식 AX=Y가 해 벡터를 갖는다
- 행렬 A의 행렬식이 0이 아니다
3-행렬식의 연산규칙
- 행렬과 전치행렬의 행렬식은 같다
- 행렬이 삼각행렬이면 대각요소의 곱으로 나타낼수있다
- 행렬 A,B,C가 $C=AB$ 이면 그 행렬식인 $det(C)=det(A)det(B)$도 성립한다
따라서 행렬식은 n차 정방행렬로 표현되는 선형 방정식계의 해의 존재성/유일성에대해 판별하는 도구가 될 수있다.
3. 선형 연립 방정식 계의 해
3.1. Recursive한 방법(n>3일때)
행렬을 3x3으로 나누어 분할정복의 방식을 사용한다(효율성은 $o(n!)$)
3.2. 크래머의 공식
nxn의 n차 정방행렬에만 적용된다. 미지수의 수와 조건행렬의 수가 같을때에만 사용가능하다.
\[AX= \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,n} \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{pmatrix} = \begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{pmatrix} = Y\]방정식의 해구하기
$x_i=\frac{det(A(i))}{det(A)}$, $i=1,2\cdots n$행렬A(i): 행렬A의 i번째 열은 벡터Y
댓글남기기